HEAP DataStructure in Java

A heap is a tree-based data structure in which all the nodes of the tree are in a specific order.

A binary heap is a complete binary tree that satisfies the heap ordering property. The ordering can be one of two types:

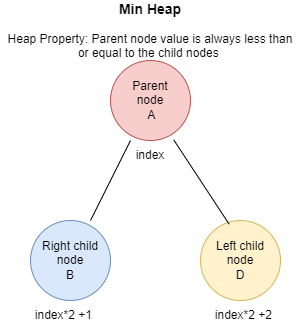
• the min-heap property: the value of each node is greater than or equal to the value of its parent, with the minimum-value element at the root.
• the max-heap property: the value of each node is less than or equal to the value of its parent, with the maximum-value element at the root.

**Note: A complete binary tree is a special type of binary tree where all the levels of the tree are filled completely except the lowest level nodes which are filled from as left as possible.

• all leaves have the same depth.
• In a complete binary tree number of nodes at depth d is 2^d. 
• In a  complete binary tree with n nodes, height of the tree is log(n+1).
• All the levels except the last level are completely full.

Heap is mostly used in algorithms that find the minimum or shortest path between two points like Dijkstra’s algorithm, to sort using heap sort, for priority queue implementations (min-heap), etc. Heaps, when used as a priority queues, can be used to remove/ find the elements with the highest or lowest priority.

A binary heap is typically represented as an array with the root element will be at arr[0]. The traversal method use to achieve Array representation is Level Order.

public class MinHeap {

private int capacity;
private int size = 0;
private int[] heap;

private MinHeap(int capacity) {
               this.capacity = capacity;
               this.heap = new int[capacity];
}

// helper methods to get the node indices
private int getLeftChildIndex(int parentIndex) { return 2 * parentIndex + 1; }
private int getRightChildIndex(int parentIndex) { return 2 * parentIndex + 2;}
private int getParentIndex(int childIndex) { return (childIndex - 1) / 2; }

// helper methods to check aif the child or parent node exists
private boolean hasLeftChild(int index) {return getLeftChildIndex(index) < size;}
private boolean hasRightChild(int index) { return getRightChildIndex(index) < size;}
private boolean hasParent(int index) { return getParentIndex(index) >= 0; }

// get child or parent nodes values
private int leftChild(int parentIndex) { return               heap[getLeftChildIndex(parentIndex)]; }
private int rightChild(int parentIndex) { return heap[getRightChildIndex(parentIndex)];
}
private int parent(int childIndex) { return heap[getParentIndex(childIndex)];
}

// Utility method: Swap indices
private void swap(int index1, int index2) {
                  int element = heap[index1];
                   heap[index1] = heap[index2];
                   heap[index2] = element;
}

// Utility method: increase array capacity if it's full
private void ensureCapacity() {
                  if (size == capacity) {
                     heap = Arrays.copyOf(heap, capacity * 2);
                     capacity = capacity * 2;}}

// Return root node in O(1) time complexity
private int peek() {
        if (size == 0) { throw new NoSuchElementException(); }
return heap[0]; 
}

// Remove the minimum node value in O(Logn) time complexity since it requires re-heapify operation
private int poll() {
        if (size == 0) { throw new NoSuchElementException(); }
        int element = heap[0];
        heap[0] = heap[size - 1];
        size--;
        heapifyDown();
 return element; 
}

//insert a new key in O(Logn) time complexity since it requires re-heapify operation
public void insert(int item) {
        ensureCapacity();
        heap[size] = item;
        size++;
        heapifyUp();
}

private void heapifyUp() {
       int index = size - 1;
   while (hasParent(index) && parent(index) > heap[index]) {
       swap(getParentIndex(index), index);
       index = getParentIndex(index);
   }
}

private void heapifyDown() {
      int index = 0;
  while (hasLeftChild(index)) {
     int smallestChildIndex = getLeftChildIndex(index);
     if (hasRightChild(index) && rightChild(index) < leftChild(index)) {
         smallestChildIndex = getRightChildIndex(index);
}
   
     if (heap[index] < heap[smallestChildIndex]) {
          break;
     } else {
          swap(index, smallestChildIndex);
     }

  index = smallestChildIndex;
  }
}

private void printHeap() {
   for (int i = 0; i < size; i++) {System.out.print(heap[i] + " ");} 
}

Priority Queue data structure in Java can be directly used to represent the min-heap which by default, implements min-heap.

PriorityQueue<Integer> pQueue = new PriorityQueue<Integer>(); 

Max heap in Java can be represented using the Priority queue by using the Collections.reverseOrder to reverse the min-heap. 

PriorityQueue<Integer> pQueue =  
             new PriorityQueue<Integer>(Collections.reverseOrder());